|
|
|
Research
|
Large-Domain
Higher-Order
Finite
Element
Modeling
of
Microwave
Devices
|
|
Largde-domain
higher-order
computational
approach
can
greatly
reduce
the
number
of
unknowns
for
a
given
problem
and
enhance
the
accuracy
and
efficiency
of
the
Finite
Element
Method
(FEM)
analysis
in
all
classes
of
applications.
This
approach
utilizes
higher-order
basis
functions
defined
in
large
geometrical
elements.
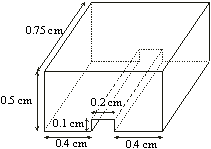
An
air-filled
rectangular
cavity
with
a
metallic
ridge
(on
the
left)
is
modeled
with
three
hexahedral
elements.
The
adopted
field-approximation
polynomial
orders
in
individual
directions
are
also
indicated. |
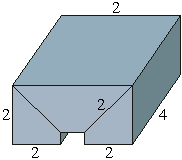
| Generalized
curvilinear
interpolatory
hexahedra
of
arbitrary
geometrical
orders,
adopted
for
the
approximation
of
geometry,
enable
excellent
curvature
modeling
(e.g.,
a
spheroid
on
the
right
is
sufficiently
accurately
modeled
by
a
single
curved
hexahedral
finite
element). |
|
|
|
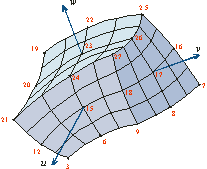
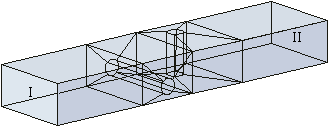
The
technique
provides
a
whole
range
of
element
shapes
(e.g.,
brick-like,
slab-like,
and
rod-like
planar
hexahedra,
as
well
as
spherically-shaped,
cylindrically-shaped,
and
elliptically-shaped
curved
hexahedra,
and
also
other
"irregular"
and/or
curved
hexahedral
shapes)
to
be
used
in
a
simulation
model
as
well.
(A
ten-element
model
of
WR-62
waveguide
with
two
crossed
cylindrical
posts
is
shown
on
the
left.) |
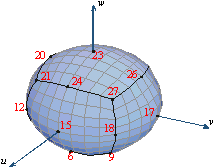
| The
hierarchical
curl-conforming
polynomial
vector
basis
functions
of
arbitrary
orders
enable
excellent
field-distribution
modeling
(e.g.,
10th-order
polynomial
field-approximation
in
the
three
parametric
coordinates
in
a
hexahedral
finite
element).
This
enables
using
as
large
as
about
2l
´
2l
´
2l
curved
FEM
hexahedra
as
building
blocks
for
modeling
of
the
electromagnetic
structure
(which
is
20
times
the
traditional
low-order
modeling
discretization
limit
of
l/10
in
each
dimension).
Calculated
reflection
coefficient
for
the
model
of
the
microwave
structure
shown
above,
with
optimal
orders
of
the
polynomial
field-approximation
in
different
elements
and
in
different
directions
in
the
range
from
2
to
5,
is
given
on
the
right. |
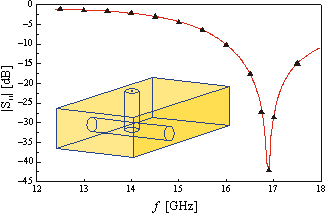
Calculated
reflection
coefficient |
|
|
|
Related
Links
|
|
Updated
April, 2008
|
