Multirate Filtering for Digital Signal Processing: MATLAB® Applications, Chapter VI: Sampling Rate Conversion by a Fractional Factor - Exercises
Contents
Exercise 6.1
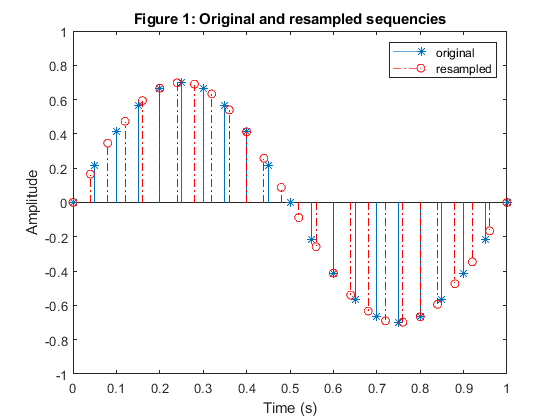
Modify program demo_6_1 to convert the sampling
frequency by the factor 5/4.
Plot the samples of input and the samples of the output signals.
Used function: resample (Signal Processing Toolbox)
clear all, close all % Sampling rate conversion by L/M = 5/4 Fx = 20; % Original sampling frequency in Hz Tx=1/Fx; % Original sampling period in seconds tx = 0:Tx:1; % Time vector tx x = 0.7*sin(2*pi*tx); % Original sequence y = resample(x,5,4); % Re-sampling ty = (0:(length(y)-1))*4*Tx/5; % New time vector ty figure (1) stem(tx,x,'*') hold on stem(ty,y,'-.r') title('Figure 1: Original and resampled sequencies') legend('original','resampled','Location','northeast') xlabel('Time (s)'), ylabel('Amplitude'), axis([0,1,-1,1])
Exercise 6.2
Use the MATLAB function upfirdn to convert the sampling rate by the factor L/M = 3/4:
a) Design an optimal FIR filter of the length
N = 64 to approximate the ideal specifications as given in
(6.2).
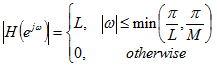. (6.2)
b) Generate 512 samples of the input signal {x[n]} given by
{x[n]}] = sin(2π0.08n) +
sin(2π0.1n) + sin(2π0.3n).
Compute the samples of the resampled signal
{y[n]}.
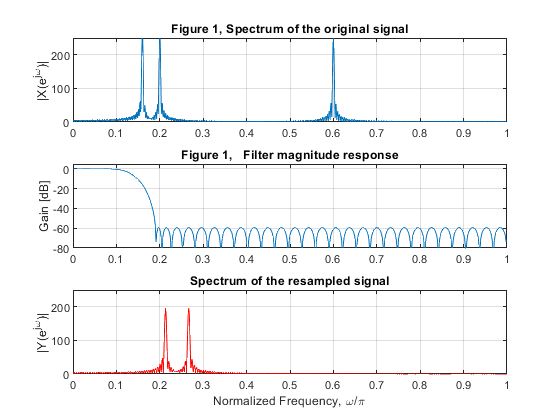
c) Plot the frequency response of the filter, and the spectrum of the signal {x[n]},
and that of the resampled signal {y[n]}.
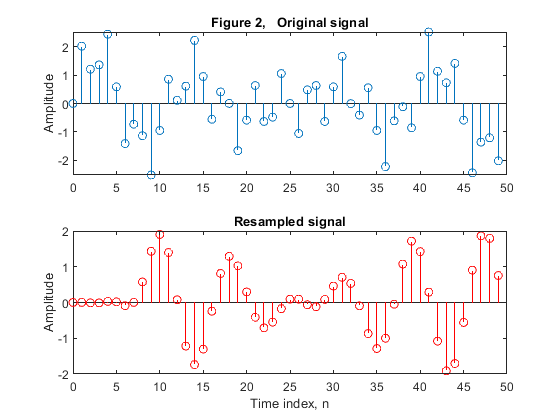
Plot the first 50 samples of the original signal,
and the first 50 samples of the resampled signal.
Comment on the results.
Used functions: upfirdn, freqz (Signal Processing Toolbox), firgr (DSP System Toolbox)
clear all, close all L=3; M=4; % Input signal x[n] n = 0:511; % Time index x1 = sin(2*pi*0.08*n); x2 = sin(2*pi*0.1*n); x3 = sin(2*pi*0.3*n); x = x1 + x2 + x3; % Generating the original signal {x[n]} [X,f] = freqz(x,1,1028,2); % Spectrum of the original signal subplot(3,1,1), plot(f,abs(X)), grid on title('Figure 1, Spectrum of the original signal') ylabel('|X(e^j^\omega)|'), axis([0,1,0,250]) % Lowpass filter specifications: to pass components x1 and x2, and to % suppress component x3: Fp>0.2/L; Fs<0.6/L N = 64; % Filter length Fp = 0.25/3; Fs = 0.19; amp = [1,1,0,0]; % Setting filter design parameters h = firgr(N-1,[0,Fp,Fs,1],amp); % Filter design [H,f]=freqz(h,1,512,2); % Computing frequency response figure (1) subplot(3,1,2), plot(f,20*log10(abs(H))), grid on title('Figure 1, Filter magnitude response') ylabel('Gain [dB]'),axis([0,1,-80,5]) % Computing resampled signal y[n] y = upfirdn(x,L*h,L,M); % Computing the resampled signal {y[n]} [Y,f] = freqz(y,1,1028,2); % Spectrum of the signal {y[n]} subplot(3,1,3), plot(f,abs(Y),'r'), grid on title('Spectrum of the resampled signal') xlabel('Normalized Frequency, \omega/\pi'), ylabel('|Y(e^j^\omega)|') axis([0,1,0,250]) figure (2) n=0:49; subplot(2,1,1) stem(n,x(1:50)),ylabel('Amplitude'), title('Figure 2, Original signal') subplot(2,1,2) stem(n,y(1:50),'r'), title('Resampled signal') xlabel('Time index, n'),ylabel('Amplitude')
Exercise 6.3
Modify program demo_6_2 to perform the sampling rate alteration with
the fractional factor L/M = 2/3.
The implementation structure is given in Figure 6.7.
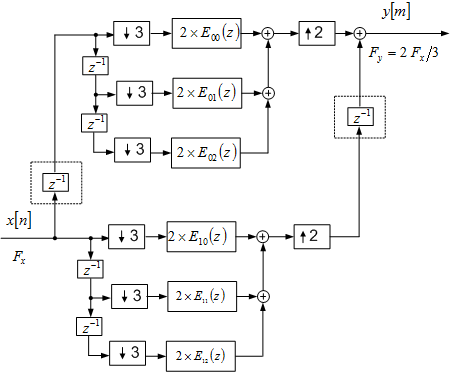
Structure of the efficient sampling-rate converter for L/M = 2/3.
(Figure 6.7 of the book).
Used functions: fir2, freqz, (Signal Processing Toolbox), firgr (DSP System Toolbox)
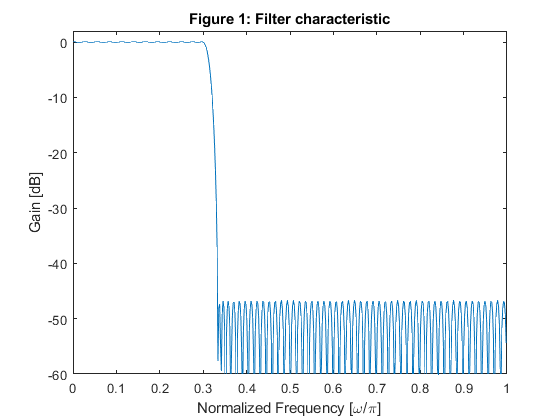
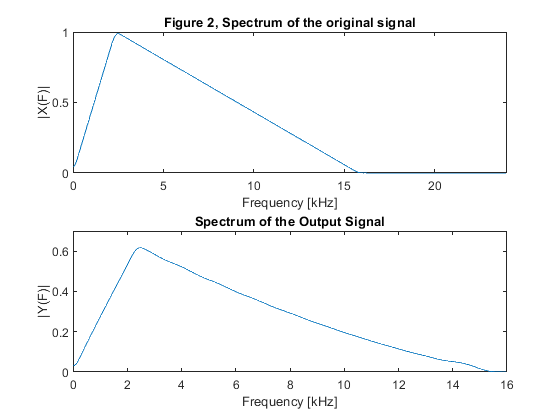
clear all, close all % Lowpass filter design N = 144; % FIR filter length Fp = 0.9/3; Fs = 1/3; amp = [1,1,0,0]; % Setting filter design parameters h = firgr(N-1,[0,Fp,Fs,1], [1,1,0,0]); % Filter design [H,f]=freqz(h,1,512,2); % Filter frequency response figure (1) plot(f,20*log10(abs(H))) xlabel('Normalized Frequency [\omega/\pi]'), ylabel('Gain [dB]') title('Figure 1: Filter characteristic') axis([0,1,-60,2]) % Generating the input signal {x[n]} L=2; M=3; Fx = 48000; Fy = 32000; F = [0,0.1,0.66,1]; m = [0,1,0,0]; % Setting the input parameters for fir2 x = fir2(255,F,m); % Generating the original signal {x[n]} [X,f] = freqz(x,1,512,Fx); % Spectrum of the original signal figure (2) subplot(2,1,1), plot(f/1000,abs(X)) xlabel('Frequency [kHz]'), ylabel('|X(F)|'), axis([0,24,0,1]) title('Figure 2, Spectrum of the original signal') % Polyphase decomposition e0 = h(1:2:length(h)); e1 = h(2:2:length(h)); E0=reshape(e0,3,length(e0)/3); E1=reshape(e0,3,length(e1)/3); % Down-sampling u1 = x; u0 = [0,x(1:length(x)-1)]; u00d = u0(1:3:length(u0)); u01d = [0,u0(3:3:length(u0))]; u02d = [0,u0(2:3:length(u0))]; u10d = u1(1:3:length(u1)); u11d = [0,u1(3:3:length(u1))]; u12d = [0,u1(2:3:length(u1))]; % Polyphase filtering x00 = filter(2*E0(1,:),1,u00d); x01 = filter(2*E0(2,:),1,u01d); x02 = filter(2*E0(3,:),1,u02d); x10 = filter(2*E1(1,:),1,u10d); x11 = filter(2*E1(2,:),1,u11d); x12 = filter(2*E1(3,:),1,u12d); yy0=x00+x01+x02; yy1=x10+x11+x12; y0ii=zeros(1,L*length(yy0)); y1ii=zeros(1,L*length(yy1)); y0ii(1:L:length(y0ii))=yy0; % Up-sampled signal y1ii(1:L:length(y1ii))=yy1; % Up-sampled signal y1 = [0,(y1ii(1:(length(y1ii)-1)))]; y = y0ii+y1; % Output signal [Y,f] = freqz(y,1,512,Fy); % Frequency response of the output signal subplot(2,1,2), plot(f/1000,abs(Y)) xlabel('Frequency [kHz]'), ylabel('|Y(F)|'), axis([0,16,0,0.7]) title('Spectrum of the Output Signal')
Exercise 6.4
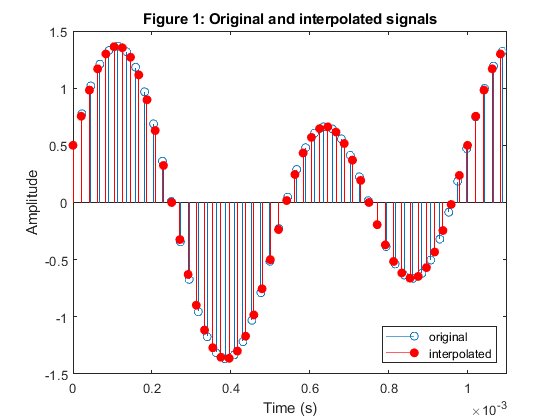
Use the MATLAB function interp1 with the option spline to convert the sampling rate of the signal x(t)=sin(2*pi*2000*t)+0.5*cos(2*pi*1000*t) from 44.1 kHz to 48 kHz.
clear all; close all; M = 147; L = 160; % Interpolation/decimation factors. Fx = 44.1e3; % Sampling frequency of the original signal: 44.1kHz Fy= Fx*L/M; % Sampling frequency of the interpolated signal n = 0:99; % Time index tx = n/Fx; % Time vector tx ty = n/Fy; % New time vector ty ny = n*L/M; x = sin(2*pi*2000*tx)+0.5*cos(2*pi*1000*tx); % Original signal {x{n*Tx)} y = interp1(tx,x,ty,'spline'); % Interpolated signal {y{n*Ty)} figure (1) stem(tx(1:49),x(1:49)); hold on stem(ty(1:54),y(1:54),'r','filled'); xlabel('Time (s)');ylabel('Amplitude');axis([0,1.1e-3,-1.5,1.5]) title('Figure 1: Original and interpolated signals') legend('original','interpolated','Location','southeast')
Exercise 6.5
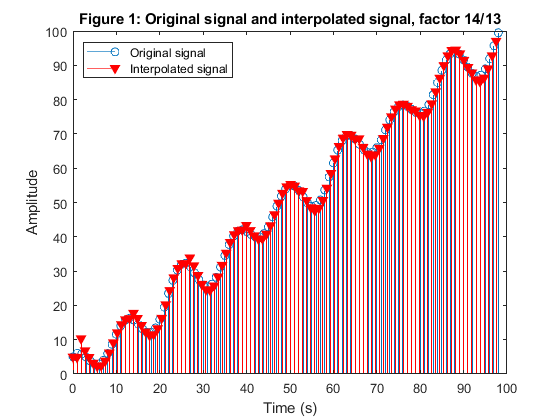
Modify program demo_6_3 (pagees 193-194 in the book) to perform the interpolation by a fractional factor 14/13 using the cubic Lagrange polynomials and the Farrow structure.
clear all, close all % Sampling-rate alteration by the fractional factor R = 14/13 % Generating the input signal {x[n]} n = -2:100; f1 = 0.1; f2 = 0.16; x = n+2*sin(pi*f1*n)+5*cos(pi*f2*n); % Original signal {x[n]} % Defining fractional intervals for sampling rate alteration by 16/15 R = 14/13; % Re-sampling factor s = 1:13; mu = [0,1-(1-1/R)*s]; mu = repmat(mu,1,8); % Vector of fractional intervals % Farrow filter, coefficients: C0 = [1/6,-1/2,1/2,-1/6]; % Vector of Lagrange coefficients for C_0(k) C1 = [0,1/2,-1,1/2]; % Vector of Lagrange coefficients for C_1(k) C2 = ([-1/6,1,-1/2,-1/3]); % Vector of Lagrange coefficients for C_2(k) C3 = [0,0,1]; % Vector of Lagrange coefficients for C_3(k) % Farrow filter, initial states: xs0 = [0,0,0]; xs1 = [0,0,0]; xs2 = [0,0,0]; xs3 = [0,0]; % Farrow filtering: l=1; for n=1:1:100 xnl = x(n+2); [v0,xs0] = filter(C0,1,xnl,xs0); [v1,xs1] = filter(C1,1,xnl,xs1); [v2,xs2] = filter(C2,1,xnl,xs2); [v3,xs3] = filter(C3,1,xnl,xs3); if mu(l)==0 y(l) = ((v0*mu(l)+v1)*mu(l)+v2)*mu(l)+x(n+2); y(l+1) = ((v0*mu(l+1)+v1)*mu(l+1)+v2)*mu(l+1)+x(n+2); l = l + 2; else y(l) = ((v0*mu(l)+v1)*mu(l)+v2)*mu(l)+x(n+2); l = l + 1; end end figure (1) tx=0:length(x)-5; % Time vector tx ty=(0:length(y)-3)*13/14; % New time vector ty stem(tx,x(3:length(x)-2)) hold on stem(ty,y(1:length(y)-2),'rv','filled') legend('Original signal','Interpolated signal','Location','northwest') xlabel('Time (s)'), ylabel('Amplitude'), title('Figure 1: Original signal and interpolated signal, factor 14/13')
Exercise 6.6
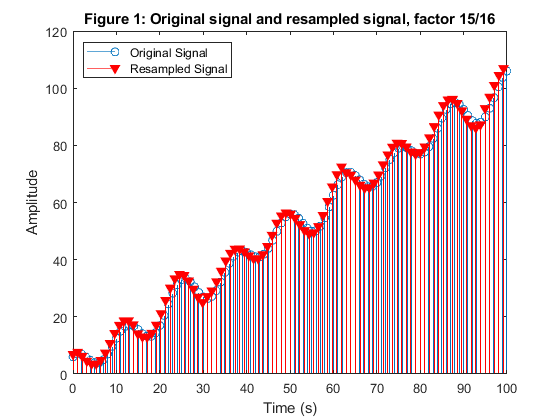
Based on the program demo_6_3 (pagees 193-194 in the book), develop the program which simulates the factor-of-15/16-decimator using the cubic Lagrange polynomials and the Farrow structure.
clear all, close all % Generating the input signal x[n] n = -2:100; % Time index f1 = 0.1; f2 = 0.16; x = n+2*sin(pi*f1*n)+5*cos(pi*f2*n)+1; % Original signal n=0:length(x)-3; tx=n; % Time vector tx % Defining fractional intervals for sampling rate alteration by 16/15 R = 15/16; % Resampling factor s = 1:14; mu = [(1/R-1)*s,0]; mu = repmat(mu,1,8); % Vector of fractional intervals % Farrow filter, coefficients: C0 = [1/6,-1/2,1/2,-1/6]; % Vector of Lagrange coefficients for C_0(k) C1 = [0,1/2,-1,1/2]; % Vector of Lagrange coefficients for C_1(k) C2 = ([-1/6,1,-1/2,-1/3]); % Vector of Lagrange coefficients for C_2(k) C3 = [0,0,1]; % Vector of Lagrange coefficients for C_3(k) % Farrow filter, initial states: xs0 = [0,0,0]; xs1 = [0,0,0]; xs2 = [0,0,0]; xs3 = [0,0]; % Farrow filtering: l=1; n=1; while n<=100 xnl = x(n+3); [v0,xs0] = filter(C0,1,xnl,xs0); [v1,xs1] = filter(C1,1,xnl,xs1); [v2,xs2] = filter(C2,1,xnl,xs2); [v3,xs3] = filter(C3,1,xnl,xs3); if mu(l)==0 y(l) = ((v0*mu(l)+v1)*mu(l)+v2)*mu(l)+x(n+3); else y(l) = ((v0*mu(l)+v1)*mu(l)+v2)*mu(l)+x(n+3); end if mu(l+1)==0 n=n+2; else n=n+1; end l=l+1; end ty=(0:(length(y)-1))/R; % New time vector ty figure (2) stem(tx,x(3:length(x))); hold on stem(ty,y(1:length(ty+1)),'rv','filled') legend('Original Signal','Resampled Signal','Location','northwest') xlabel('Time (s)'), ylabel('Amplitude') title('Figure 1: Original signal and resampled signal, factor 15/16') % Comment: % In the case of R = 15/16 we have lowering of the sampling frequency (Fx>Fy) meaning % that Ty<Tx. Therefore, the basepoint index nl become ny=nx+1 (as 1/R % >1) and 1/R=1+mu. The parameter mu should take values from 1/15 to 14/15, and each % 15th sample of x would be missed as mu can't take value of mu=1. So, in % this program the sample x[15] should not be used as the input sample for the Farrow filter structure. % We have jumped over x[15] continuing interpolation process from x[16] with mu=0. % As ny=nx+1, we'll have that xnl=x[n+1+N/2]=x[n+3].
Exercise 6.7
Modify program demo_6_4 (page 197 in the book)
for fractional delay filtering by means of the Farrow structure.
Recall that the input and the output rates in the case of a fractional
filter are identical.
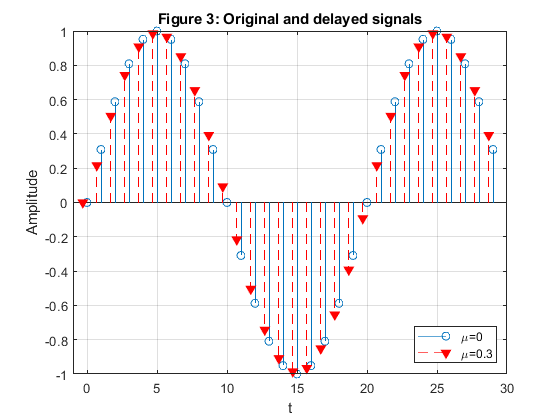
Generate the first 30 samples of the signal x[n] = sin(0.1*pi*n)
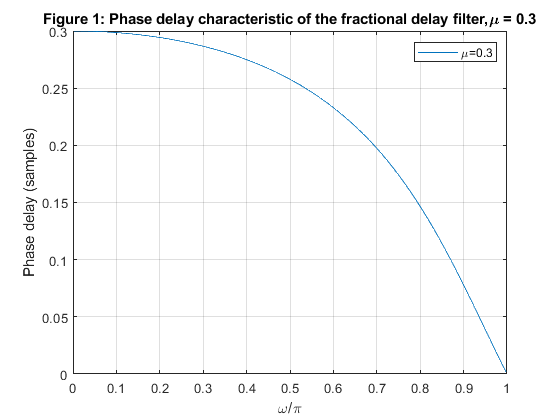
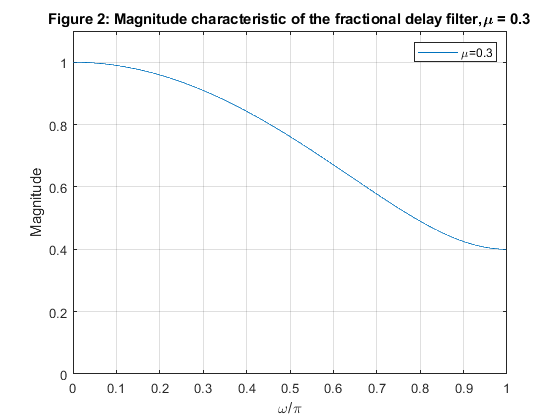
and perform the fractional delay filtering for the delay factor μ =
0.3.
Plot the input sequence {x[n]} and the delayed sequence {y[n]}.
Used functions: freqz, phasedelay (Signal Processing Toolbox), dfilt.farrowlinearfd (DSP System Toolbox)
clear all, close all mu = 0.3; h = dfilt.farrowlinearfd(mu); % Design object for Farrow fractional delay filtering [phi,f] = phasedelay(h,512,2); % Computing the phase delay figure (1) plot(f,phi/pi) xlabel('\omega/\pi'), ylabel('Phase delay (samples)'), grid title('Figure 1: Phase delay characteristic of the fractional delay filter,\mu = 0.3') legend('\mu=0.3','Location','northeast'); [H,f] = freqz(h,512,2); % Computing the frequency response figure (2) plot(f,abs(H)) xlabel('\omega/\pi'), ylabel('Magnitude'), axis([0,1,0,1.1]),grid title('Figure 2: Magnitude characteristic of the fractional delay filter,\mu = 0.3') legend('\mu=0.3','Location','northeast'); % Aplying the fractional delay filter t = 0:29; x = sin(pi*0.1*t); % Original signal y = filter(h,x); % Delayed signal figure (3) stem(t,x); hold on; stem(t-0.3,y,'v--r','filled') xlabel('t'),ylabel('Amplitude') title('Figure 3: Original and delayed signals') legend('\mu=0','\mu=0.3','Location','southeast'), grid axis([-1,30,-1,1]);
