Multirate Filtering for Digital Signal Processing: MATLAB® Applications, Chapter III: Filters in Multirate Systems - Exercises
Contents
Exercise 3.1
Design an optimal linear-phase FIR filter to satisfy the
Case a tolerance scheme of Figure 3.5 (a), for the sampling-rate
conversion factor M = 4.
The peak passband ripple is ap = 0.1 dB,
and the minimal stopband attenuation is as = 50 dB.
Choose the passband edge frequency ωp <π/M.
Compute and plot: impulse response, magnitude response, phase response, and pole-zero locations.
Used functions: firpmord, firpm (Signal Processing Toolbox)
clear all; close all; M = 4; % Decimation factor M ap = 0.1; as = 50; Fs = 1/M; % Filter specifications % Fp = input('Choose the FIR filter passband edge frequency Fp<0.25: '); Fp = 0.1; dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies A = [1 0]; % Desired amplitudes [Nord,Fo,Ao,W] = firpmord(F,A,dev); % Estimating the filter order Nord=Nord+0; % Correction of the Nord when calculated value % by firpmord function doesn't satisfy the Case a tolerance, so that designed filter fails to meet the requested stopband attenuation h = firpm(Nord,Fo,Ao,W); % Filter coefficients based on Parks-McClellan algorithm figure(1), freqz(h,1,1024), % Computes and plots the frequency response axis([0,1,-80,5]), grid on; figure(2), subplot(2,1,1), impz(h,1); % Plots the impulse response subplot(2,1,2), zplane(h,1); % Pole/zero plot
Exercise 3.2
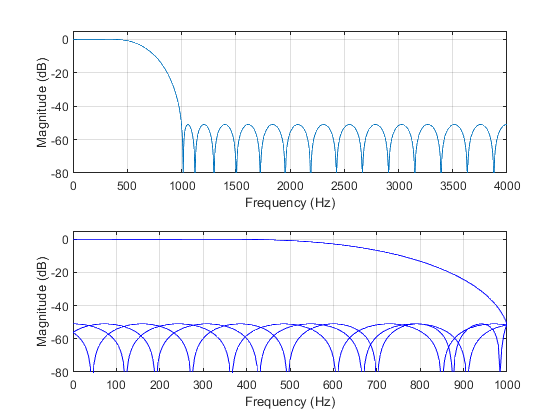
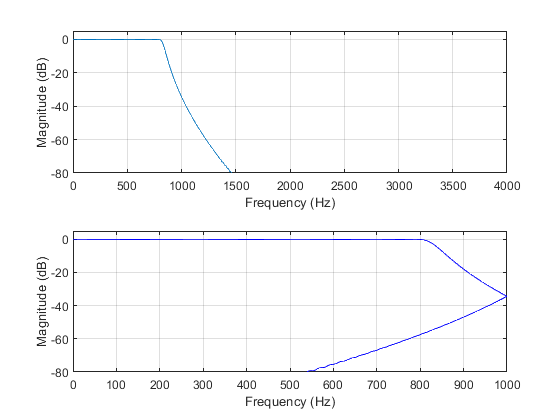
Compute and plot the aliasing characteristics of the 4-fold-decimator with
antialiasing filter from Exercise 3.1.
FIR filter: Coefficeints are computed by firpm function
according to the filter characteristics from Exercise 3.1.
Sampling frequencies: input Fx=8000 Hz, output Fy=2000 Hz.
Decimation factor M=4.
Used functions: firpmord, firpm (Signal Processing Toolbox)
clear all; close all; M = 4; % Decimation factor ap = 0.1; as = 50; Fs = 1/M; % Filter specifications Fp = 0.1; dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies A = [1 0]; % Desired amplitudes [Nord,Fo,Ao,W] = firpmord(F,A,dev); % Estimating the filter order h = firpm(Nord,Fo,Ao,W); % Filter coefficients n = 0:length(h)-1; % Time index Fx = 8000; % Input sampling frequency (Hz) Fy = Fx/M; % Output sampling frequency (Hz) % Computing the filter magnitude response for r=1:1001 F(r) = (r-1)*Fx/2000; omega = 2*pi*F(r)/Fx; W = exp(-i*n*omega); H(r) = sum(h.*W); end figure(3), subplot(2,1,1), plot(F,20*log10(abs(H))), xlabel('Frequency (Hz)'), ylabel('Magnitude (dB)'), axis([0,4000,-80,5]), grid % Computing the unaliased characteristic and 4 aliased characteristics according to (3.30) subplot(2,1,2), k = 0; for l=1:4 for r=1:251 FF(r) = (r-1)*Fy/500; omega = 2*pi*FF(r)/Fy; W = exp(-i*n*(omega-2*k*pi)/M); Hal(r) = sum(h.*W); end k = k + 1; plot(FF,20*log10(abs(Hal)),'b'), hold on, end xlabel('Frequency (Hz)'), ylabel('Magnitude (dB)'), axis([0,1000,-80,5]), grid on, hold off;
Exercise 3.3
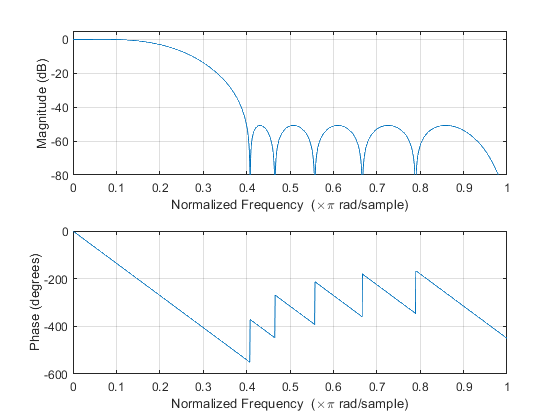
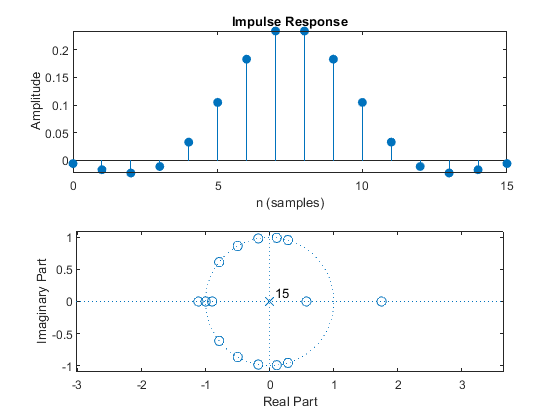
Design an optimal linear-phase FIR filter to satisfy the
Case b tolerance scheme of Figure 3.5 (b), for the sampling-rate
conversion factor M = 4.
The peak passband ripple is ap = 0.1 dB,
and the minimal stopband attenuation is as = 50 dB.
Choose the passband edge frequency ωp <
π/M.
Compute and plot: impulse response, magnitude response, phase response, and pole-zero locations.
Used functions: firpmord, firpm (Signal Processing Toolbox)
clear all; close all; M=4; %Decimation factor M ap = 0.1; as = 50; %Fp = input('Choose the FIR filter passband edge frequency Fp<0.25: '); Fp = 0.1; Fs = 2/M-Fp; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies A = [1 0]; % Desired amplitudes [Nord,Fo,Ao,W] = firpmord(F,A,dev); % Estimating the filter order Nord = Nord+0; %Correction of the Nord when calculated value doesn't satisfy the Case b tolerance h = firpm(Nord,Fo,Ao,W); % Computing the filter coefficients figure(1), freqz(h,1,1024), % Computes and plots the frequency response axis([0,1,-80,5]); figure(2), subplot(2,1,1), impz(h,1); % Plots the impulse response subplot(2,1,2), zplane(h,1); % Pole/zero plot
Exercise 3.4
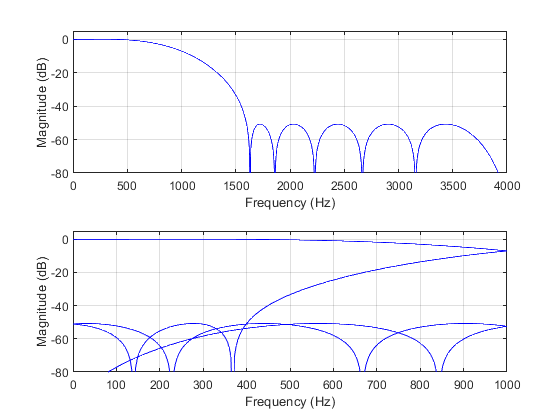
Compute and plot the aliasing characteristics of the 4-fold-decimator with
antialiasing filter from Exercise 3.3.
FIR filter: Coefficeints are computed by firpm
function according to the filter characteristics from Exercise 3.3.
Sampling frequencies: input Fx=8000 Hz, output Fy=2000 Hz. Decimation
factor M=4.
Used functions: firpmord, firpm (Signal Processing Toolbox)
clear all; close all; M = 4; % Decimation factor ap = 0.1; as = 50; Fp = 0.1; Fs = 2/M-Fp; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies A = [1 0]; % Desired amplitudes [Nord,Fo,Ao,W] = firpmord(F,A,dev); % Estimating the filter order h = firpm(Nord,Fo,Ao,W); % Filter coefficients n = 0:length(h)-1; % Time index Fx = 8000; % Input sampling frequency (Hz) Fy = Fx/M; % Output sampling frequency (Hz) % Computing the filter magnitude response for r=1:1001 F(r) = (r-1)*Fx/2000; omega = 2*pi*F(r)/Fx; W = exp(-i*n*omega); H(r) = sum(h.*W); end figure(3), subplot(2,1,1), plot(F,20*log10(abs(H)),'b'), xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)'), axis([0,4000,-80,5]), grid; % Computing the unaliased characteristic and 4 aliased characteristics according to (3.30) subplot(2,1,2), k = 0; for l=1:4 for r=1:251 FF(r) = (r-1)*Fy/500; omega = 2*pi*FF(r)/Fy; W = exp(-i*n*(omega-2*k*pi)/M); Hal(r) = sum(h.*W); end k = k + 1; plot(FF,20*log10(abs(Hal)),'b'), hold on, end xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)'), axis([0,1000,-80,5]), grid on, hold off;
Exercise 3.5
Design an optimal linear-phase FIR filter to satisfy the
Case c tolerance scheme of Figure 3.5 (c), for the sampling-rate
conversion factor M = 4.
The peak passband ripple is ap = 0.1 dB,
and the minimal stopband attenuation is as = 50 dB.
Choose the passband edge frequency ωp <
π/M.
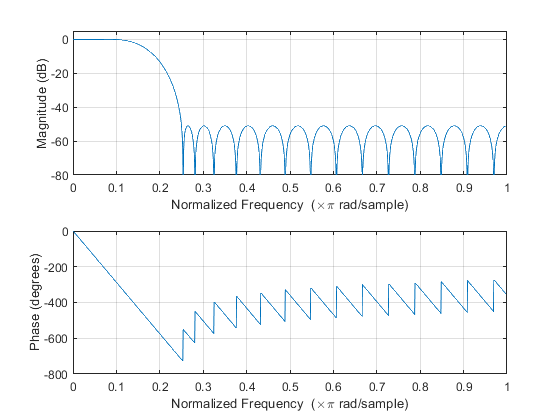
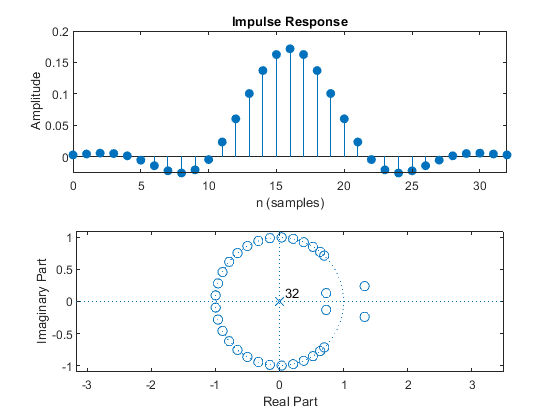
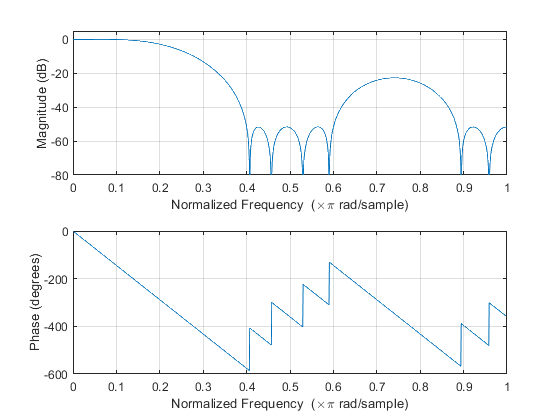
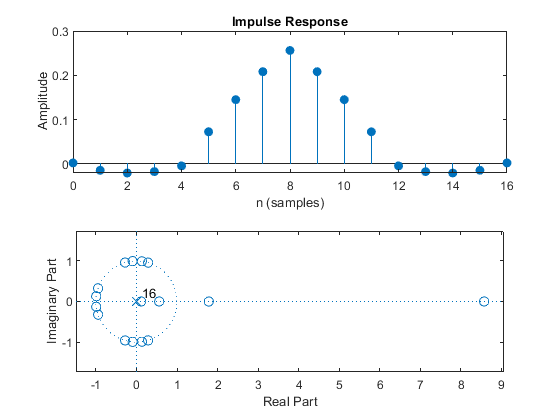
Compute and plot: impulse response, magnitude response, phase response, and pole-zero locations.
Used functions: firpmord, firpm (Signal Processing Toolbox)
clear all; close all; M = 4; %Decimation factor M ap = 0.1; as = 50; % Filter specifications Fp = 0.1; devp = (10^(ap/20)-1)/(10^(ap/20)+1); % Passband ripple devs = 10^(-as/20); % Stopband ripple Fop = [0, Fp]; % Passband boundary frequencies Fos1 = [2/M-Fp,2/M+Fp]; % Stopband 1 boundary frequencies Fos2 = [4/M-Fp,min(4/M+Fp,1)]; % Stopband 2 boundary frequencies Fo= [Fop, Fos1, Fos2]; % Vector of normalized frequency points Ao = [1,1,0,0,0,0]; % Desired amplitudes W = [1, devp/devs, devp/devs]; % Estimating the filter order Nord = 16; h = firpm(Nord,Fo,Ao,W); % Computing the filter coefficients figure(1),freqz(h,1,1024), % Computes and plots the frequency response axis([0,1,-80,5]); figure(2), subplot(2,1,1),impz(h,1); % Plots the impulse response subplot(2,1,2),zplane(h,1); % Pole/zero plot
Exercise 3.6
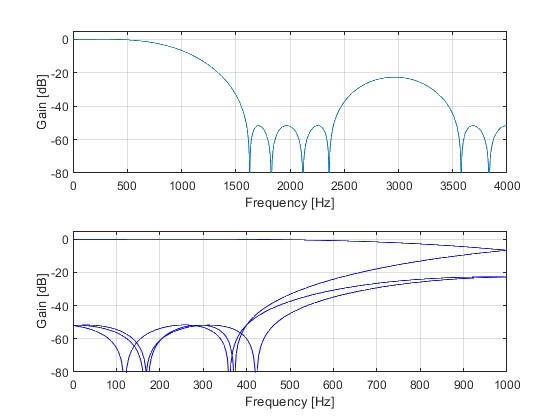
Compute and plot the aliasing characteristics of the 4-fold-decimator with
antialiasing filter from Exercise 3.5.
FIR filter: Coefficeints are computed by firpm
function according to the filter characteristics from Exercise 3.5.
Sampling frequencies: input Fx=8000 Hz, output Fy=2000 Hz.. Decimation
factor M=4.
Used functions: firpmord, firpm (Signal Processing Toolbox)
clear all; close all; M = 4; % Decimation factor ap = 0.1; as = 50; Fp = 0.1; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples Fop = [0, Fp]; % Passband boundary frequencies Fos1 = [2/M-Fp,2/M+Fp]; % Stopband 1 boundary frequencies Fos2 = [4/M-Fp,min(4/M+Fp,1)]; % Stopband 2 boundary frequencies Fo= [Fop, Fos1, Fos2]; % Vector of normalized frequency points Ao = [1,1,0,0,0,0]; % Desired amplitudes W = [1, dev(1)/dev(2), dev(1)/dev(2)]; % Estimating the filter order Nord = 16; h = firpm(Nord,Fo,Ao,W); % Filter coefficients n = 0:length(h)-1; % Time index Fx = 8000; % Input sampling frequency (Hz) Fy = Fx/M; % Output sampling frequency (Hz) % Computing the filter magnitude response for r=1:1001 F(r) = (r-1)*Fx/2000; omega = 2*pi*F(r)/Fx; W = exp(-i*n*omega); H(r) = sum(h.*W); end figure(3), subplot(2,1,1),plot(F,20*log10(abs(H))), xlabel('Frequency [Hz]'),ylabel('Gain [dB]'), axis([0,4000,-80,5]),grid on; % Computing the unaliased characteristic and 3 aliased characteristics according to (3.30) subplot(2,1,2), k = 0; for l=1:4 for r=1:251 FF(r) = (r-1)*Fy/500; omega = 2*pi*FF(r)/Fy; W = exp(-i*n*(omega-2*k*pi)/M); Hal(r) = sum(h.*W); end k = k + 1; plot(FF,20*log10(abs(Hal)),'b'),hold on, end xlabel('Frequency [Hz]'),ylabel('Gain [dB]'), axis([0,1000,-80,5]),grid on,hold off;
Exercise 3.7
Design an elliptic IIR filter to satisfy the
Case b tolerance scheme of Figure 3.5 (b), for the sampling-rate
conversion factor M = 4.
The peak passband ripple is ap = 0.1 dB,
and the minimal stopband attenuation is as = 50 dB.
Choose the passband edge frequency ωp < π/M
.
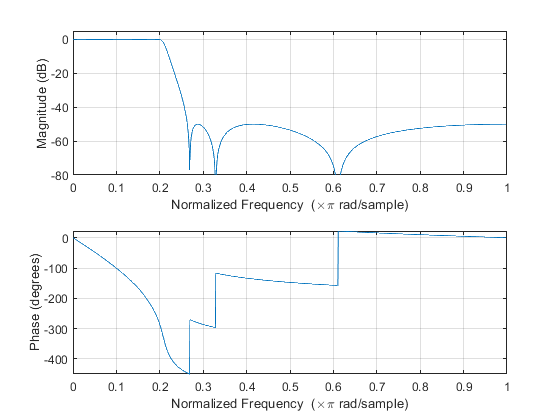
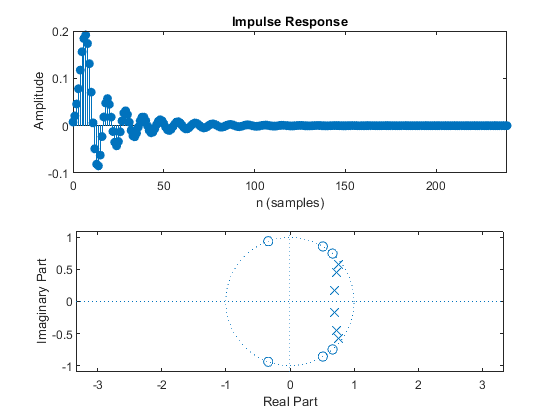
Compute and plot: impulse response, magnitude response, phase response, and pole-zero locations.
Used functions: ellipord, ellip (Signal Processing Toolbox)
clear all; close all; M=4; %Decimation factor M ap = 0.1; as = 50; Fp = 0.2; Fs = 2/M-Fp; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies [N,Fn] = ellipord(Fp,Fs,ap,as); % Estimating the filter order [B,A] = ellip(N,ap,as,Fn); % Elliptic filter design figure (1), freqz(B,A,1024), % Computes and plots the frequency response axis([0,1,-80,5]), figure (2), subplot(2,1,1), impz(B,A); % Plots the impulse response of designed eliptic IIR filter subplot(2,1,2), zplane(B,A); % Pole/zero plot
Exercise 3.8
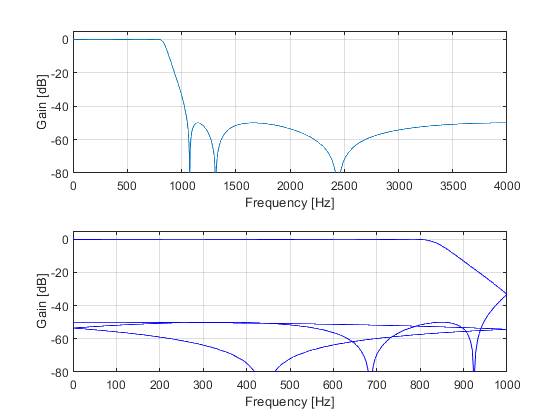
Compute and plot the aliasing characteristics of
the 4-fold-decimator with IIR antialiasing filter from Exercise 3.7.
Sampling frequencies: input Fx=8000 Hz, output Fy=2000 Hz.
Decimation factor M=4.
Used functions: ellipord, ellip (Signal Processing Toolbox)
clear all;close all M = 4; % Decimation factor ap = 0.1; as = 50; Fp = 0.2; Fs = 2/M-Fp; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies [N,Fn] = ellipord(Fp,Fs,ap,as); % Estimating the filter order [B,A] = ellip(N,ap,as,Fn); % Elliptic filter design [h,F]=impz(B,A); n = (0:length(h)-1)'; % Time index Fx = 8000; % Input sampling frequency (Hz) Fy = Fx/M; % Output sampling frequency (Hz) % Computing the filter magnitude response for r=1:1001 F(r) = (r-1)*Fx/2000; omega = 2*pi*F(r)/Fx; W = exp(-i*n*omega); H(r) = sum(h.*W); end figure(3), subplot(2,1,1),plot(F,20*log10(abs(H))), xlabel('Frequency [Hz]'),ylabel('Gain [dB]'), axis([0,4000,-80,5]),grid on; % Computing the unaliased characteristic and 3 aliased characteristics according to (3.30) subplot(2,1,2), k = 0; for l=1:4 for r=1:251 FF(r) = (r-1)*Fy/500; omega = 2*pi*FF(r)/Fy; W = exp(-i*n*(omega-2*k*pi)/M); Hal(r) = sum(h.*W); end k = k + 1; plot(FF,20*log10(abs(Hal)),'b'),hold on, end xlabel('Frequency [Hz]'),ylabel('Gain [dB]'), axis([0,1000,-80,5]),grid on,hold off;
Exercise 3.9
Design a Chebyshev IIR filter to satisfy the
Case b tolerance scheme of Figure 3.5 (b), for the sampling-rate
conversion factor M = 4.
The peak passband ripple is ap = 0.1 dB, and the minimal stopband attenuation is as = 50 dB. Choose the passband edge frequency
ωp < π/M.
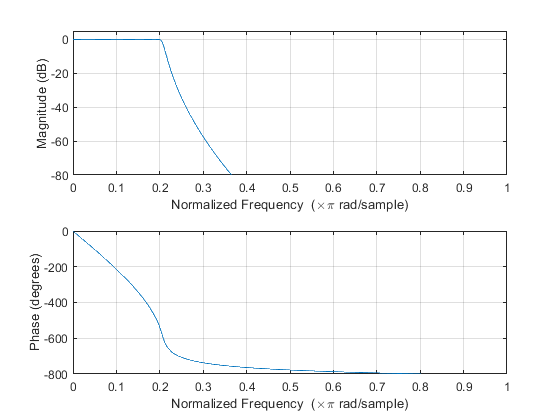
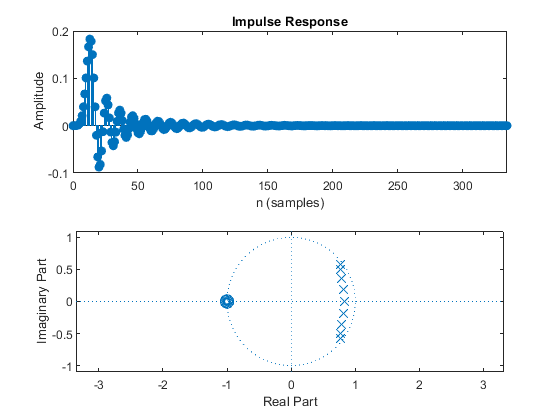
Compute and plot: impulse response, magnitude response, phase response, and pole-zero locations.
Used functions: cheb1ord, cheby1 (Signal Processing Toolbox)
clear all; close all; M=4; %Decimation factor M ap = 0.1; as = 50; Fp = 0.2; Fs = 2/M-Fp; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies [N,Fn] = cheb1ord(Fp,Fs,ap,as); % Estimating the filter order [B,A] = cheby1(N,ap,Fn); % Chebyshev filter design figure (1), freqz(B,A,1024), % Computes and plots the frequency response axis([0,1,-80,5]), figure (2), subplot(2,1,1), impz(B,A); % Plots the impulse response of designed eliptic IIR filter subplot(2,1,2), zplane(B,A); % Pole/zero plot
Exercise 3.10
Compute and plot the aliasing characteristics of
the 4-fold-decimator with IIR antialiasing filter from Exercise 3.9.
Sampling frequencies: input Fx=8000 Hz, output Fy=2000 Hz.
Decimation factor M=4.
Used functions: cheb1ord, cheby1 (Signal Processing Toolbox)
clear all; close all; M = 4; % Decimation factor ap = 0.1; as = 50; Fp = 0.2; Fs = 2/M-Fp; % Filter specifications dev = [(10^(ap/20)-1)/(10^(ap/20)+1), 10^(-as/20)]; % Passband and stopband ripples F = [Fp Fs]; % Cutoff frequencies [N,Fn] = cheb1ord(Fp,Fs,ap,as); % Estimating the filter order [B,A] = cheby1(N,ap,Fn); % Chebyshev filter design [h,F]=impz(B,A); n = (0:length(h)-1)'; % Time index Fx = 8000; % Input sampling frequency (Hz) Fy = Fx/M; % Output sampling frequency (Hz) % Computing the filter magnitude response for r=1:1001 F(r) = (r-1)*Fx/2000; omega = 2*pi*F(r)/Fx; W = exp(-i*n*omega); H(r) = sum(h.*W); end figure(3), subplot(2,1,1), plot(F,20*log10(abs(H))), xlabel('Frequency (Hz)'), ylabel('Magnitude (dB)'), axis([0,4000,-80,5]), grid; % Computing the unaliased characteristic and 4 aliased characteristics according to (3.30) subplot(2,1,2), k = 0; for l=1:4 for r=1:251 FF(r) = (r-1)*Fy/500; omega = 2*pi*FF(r)/Fy; W = exp(-i*n*(omega-2*k*pi)/M); Hal(r) = sum(h.*W); end k = k + 1; plot(FF,20*log10(abs(Hal)),'b'), hold on, end xlabel('Frequency (Hz)'), ylabel('Magnitude (dB)'), axis([0,1000,-80,5]), grid on, hold off;
Exercise 3.11
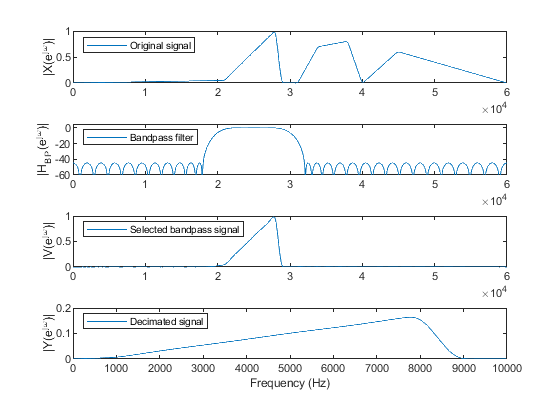
Modify program demo_3_2 to study the integer-band decimation for the factor M = 6, and the input
sampling frequency of 120 kHz.
Select frequency band 20000-28000 kHz.
Used functions: downsample, fir2 (Signal Processing Toolbox), firgr (DSP System Toolbox)
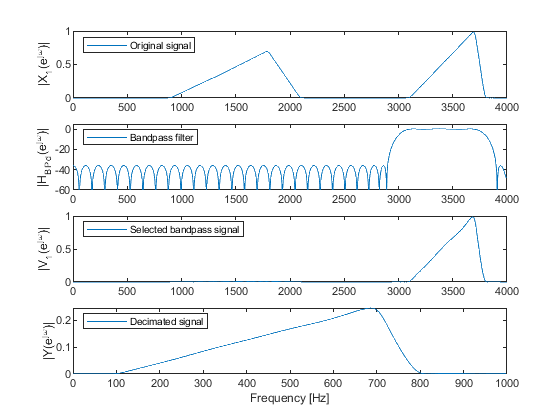
clear all; close all; Fx = 120000; M = 6; Fy = Fx/M; F = [0,21000/60000,28000/60000,29000/60000,31000/60000,34000/60000,38000/60000,40000/60000,45000/60000,1]; A = [0,0.05,1,0,0,0.7,0.8,0,0.6,0]; x = fir2(511,F,A); % Generating the input signal signal ‘x’ [X,f] = freqz(x,1,1024,Fx); % Computing the spectrum of the signal ‘x’ figure(1), subplot(4,1,1), plot(f,abs(X)), ylabel('|X(e^j^\omega)|'); legend('Original signal','Location','northwest') % Setting the band pass filter to satisfy Eqs (3.32) and (3.33) for k =2. ABp = [0,0,1,1,0,0]; % Desired magnitude response FBp = [0,18000/60000,22000/60000,28000/60000,32000/60000,1];% Boundary frequencies hBP = firgr(68,FBp,ABp); % Bandpass filter design [HBP,f] = freqz(hBP,1,1024,Fx); % Computing the bandpass filter frequency response subplot(4,1,2), plot(f,20*log10(abs(HBP))), ylabel('|H_B_P(e^j^\omega)|'), axis([0,60000,-60,5]); legend('Bandpass filter','Location','northwest') v = filter(hBP,1,x); % Bandpass filtering [V,f] = freqz(v,1,1024,Fx); % Computing the spectrum of the bandpass signal subplot(4,1,3), plot(f,abs(V)), ylabel('|V(e^j^\omega)|'); legend('Selected bandpass signal','Location','northwest') y = downsample(v,M); % Down-sampling of the bandpass signal [Y,ff] = freqz(y,1,1024,Fy); % Computing the spectrum of the decimated signal subplot(4,1,4); plot(ff,abs(Y)), xlabel('Frequency (Hz)'), ylabel('|Y(e^j^\omega)|'); legend('Decimated signal','Location','northwest')
Exercise 3.12
Using the integer-band decimation and the integer-band interpolation, develop the MATLAB program
which translates the selected band of frequencies into a desired position.
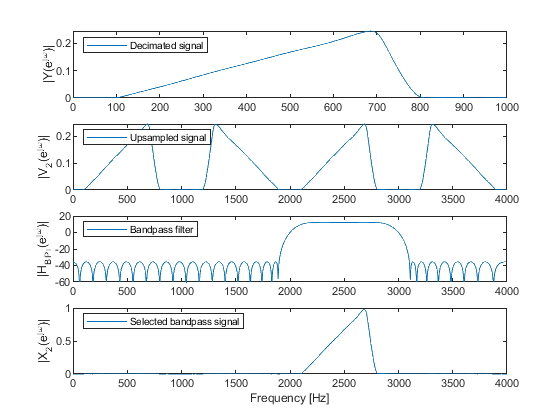
clear all; close all; % This program is created to translate the bandpass signal from the range 3000 - 4000 Hz to the range 2000 - 3000 Hz. % The sampling frequency is 8000 Hz, and conversion factors M = L =4. Fx = 8000; M = 4; Fy = Fx/M; F = [0,900/4000,1300/4000,1800/4000,2100/4000,2800/4000,3100/4000,3700/4000,3800/4000,1]; A = [0,0,0.3,0.7,0,0,0,1,0,0]; x1 = fir2(511,F,A); % Generating the input signal signal ‘x’ [X1,f] = freqz(x1,1,1024,Fx); % Computing the spectrum of the signal ‘x’ figure(1), subplot(4,1,1), plot(f,abs(X1)),ylabel('|X_1(e^j^\omega)|'), legend('Original signal','Location','northwest'); hBPd = firgr(68,[0,2900/4000,3100/4000,3700/4000,3900/4000,1],[0,0,1,1,0,0]); % Bandpass filter design [HBPd,f] = freqz(hBPd,1,1024,Fx); % Computing the bandpass filter frequency response subplot(4,1,2), plot(f,20*log10(abs(HBPd))) legend('Bandpass filter','Location','northwest') ylabel('|H_B_P_d(e^j^\omega)|'),axis([0,4000,-60,5]); v1 = filter(hBPd,1,x1); % Bandpass filtering [V1,f] = freqz(v1,1,1024,Fx); % Computing the spectrum of the bandpass signal subplot(4,1,3), plot(f,abs(V1)),ylabel('|V_1(e^j^\omega)|'), legend('Selected bandpass signal','Location','northwest'); y = downsample(v1,M); % Down-sampling of the bandpass signal n = 0:length(y)-1; y = y.*(-1).^n; % Inverting the spectrum of the decimated signal (case k1=3, an odd number) [Y,ff] = freqz(y,1,1024,Fy); % Computing the spectrum of the decimated signal subplot(4,1,4); plot(ff,abs(Y)), legend('Decimated signal','Location','northwest'), ylabel('|Y(e^j^\omega)|'),xlabel('Frequency [Hz]'); % Integer-band interpolation (M=4, k2=2) Fy = 2000; L = 4; Fz = 8000; hBPi=L*firgr(64,[0,1900/4000,2200/4000,2800/4000,3100/4000,1],[0,0,1,1,0,0]); % Bandpass filter design v2 = upsample(y,L); % Up-sampling [V2,f] = freqz(v2,1,1024,Fz); % Spectrum of the up-sampled signal figure(2), subplot(4,1,1),plot(ff,abs(Y)),ylabel('|Y(e^j^\omega)|'), legend('Decimated signal','Location','northwest'), subplot(4,1,2),plot(f,abs(V2)),ylabel('|V_2(e^j^\omega)|'), legend('Upsampled signal','Location','northwest'); [HBPi,f] = freqz(hBPi,1,1024,Fz); % Computing the bandpass filter frequency response subplot(4,1,3) ,plot(f,20*log10(abs(HBPi))), ylabel('|H_B_P_i(e^j^\omega)|'),axis([0,4000,-60,20]); legend('Bandpass filter','Location','northwest'), x2 = filter(hBPi,1,v2); % Filtering [X2,f] = freqz(x2,1,1024,Fz); % Computing the spectrum of the bandpass interpolated signal subplot(4,1,4), plot(f,abs(X2)), ylabel('|X_2(e^j^\omega)|'),xlabel('Frequency [Hz]'), legend('Selected bandpass signal','Location','northwest','Location','northwest');