 Ласло Краус
Ласло КраусПрви парцијални испит
3. 7. 1999.
 Ласло Краус
Ласло Краус |
ПЈМП Први парцијални испит 3. 7. 1999. |
|---|
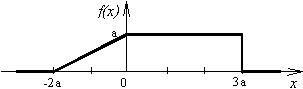 Саставити потпрограм за генерисање псеудослучајних бројева чија је
густина расподеле вероватноће приказана на слици. На располагању стоји
генератор псеудослучајних бројева са униформном расподелом.
Саставити потпрограм за генерисање псеудослучајних бројева чија је
густина расподеле вероватноће приказана на слици. На располагању стоји
генератор псеудослучајних бројева са униформном расподелом.A, B, C, ...,
H кодирају се са по три бита 000,
001, 010, ..., 111. Извршити
компресију низа симбола ADEA DGAD
GDEG AG применом LZW поступка.
Добијени резултат проверити применом инверзног поступка на добијени низ
битова.
predmet(
Naziv, Semestar), student(
Ime, Semestar) и ocena(
Student, Predmet, Ocena).
Студент може да има више оцена из истог предмета ако је испит полагао
више пута. Саставити правила на Prolog-у помоћу којих могу да се
добију одговори на питања Из ког предмета је студент положио
испит?, Из ког предмета је студент пао на испиту? и Из
ког премета студент треба да полаже испит?.
podaci( [[1,5], [2,1],
[3,2], [2,4], [2,7],
[1,6]], 2, [1,4,7]).
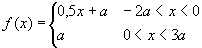
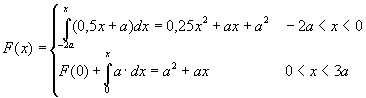
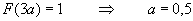
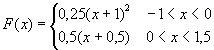
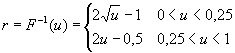
#include <math.h>
double urng ();
double rng () {
double u=urng();
return u<0.25 ? 2*sqrt(u)-1 : 2*u-0.5;
}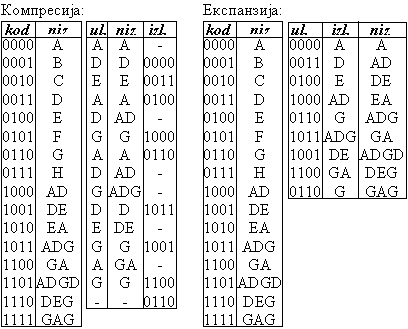
Резултујући код: 0000 0011 0100 1000 0110 1011
#define N 8
void jpeg(int a[N][N], int b[N*N]){
int i, j, k, l, m, smer=1;
for (m=k=0; k<2*N-1; k++) {
if (smer == 1) { i = k<N ? k : N-1; j = k - i; }
else { j = k<N ? k : N-1; i = k - j; }
for (l=0; l<=((k<N)?(k):(2*N-2-k)); l++)
{ b[m++] = a[i][j]; i -= smer; j += smer; }
smer = -smer;
}
}#include <gks.h>
void main ()
enum { N = 200 };
int rs_tip=GWS_VT340, i;
float a, fimax, r, fi, dfi;
Gpoint tacke[N+1];
Glimit prozor;
scanf ("%f%f", &a, &fimax);
prozor.xmin = prozor.ymin =
- (prozor.xmax = prozor.ymax =
r = a*fimax);
gopengks (0, 0);
gopenws (10, "tt:", &rs_tip);
gactivatews (10);
gsetwindow (1, &prozor);
gseltran (1);
tacke[0].y = tacke[1].y = 0;
tacke[0].x = -(tacke[1].x = r);
gpolyline (2, tacke);
tacke[0].x = tacke[1].x = 0;
tacke[0].y = -(tacke[1].y = r);
gpolyline (2, tacke);
dfi = fimax / N;
for (i=0; i<=N; i++) {
r = a * (fi = i * dfi);
tacke[i].x = r * cos (fi);
tacke[i].y = r * sin (fi);
}
gpolyline (N+1, tacke);
gdeactivatews (10);
gclosews (10);
gclosegks ();
}polozio(Student,Predmet) :-
ocena(Student,Predmet,Ocena),
Ocena >= 6;
pao(Student,Predmet) :-
ocena(Student,Predmet,Ocena),
Ocena < 6;
treba(Student,Predmet) :-
student(Student,SemestarS),
predmet(Predmet,SemestarP),
SemestarP =< SemestarS,
not(polozio(Student,Predmet)).podaci([],_,[]).
podaci([[S,P]|R1],S,[P|R2]) :-
podaci(R1,S,R2), !.
podaci([_|R1],S,R2) :-
podaci(R1,S,R2).
Copyright © 2001, Laslo Kraus
Последња ревизија: 15.7.1999.