Ласло Краус	ИР2ОО1 Колоквијум 27. 11. 2010.

Поставка задатка 1 (30 поена) (⇒ почетак)

Одговорити концизно (по једна или две реченице) и прецизно на следећа питaња:

а) Да ли је на месту на којем још није дефинисана класа X дозвољено писати:

1. X x;      class X;
2. class X;  X x;
3. X* px;    class X;
4. class X;  X* px;

б) За коју од метода класе X, чије су декларације наведене, имплицитна декларација показивача this је: const X* const this;

1. static void m(const X&);
2. const X& m();
3. void m() const;

в) Написати могуће декларације операторске функције + у класи X која ће се примењивати у изразима , где су i податак целобројног типа (int), a x објекат класног типа X.

Поставка задатка 2 (укупно 70 поена) (⇒ решење | почетак)

Написати на језику C++ следеће класе (класе опремити оним конструкторима, деструктором и оператором за доделу вредности, који су потребни за безбедно коришћење класа):

• (30 поена) Тачка у равни се задаје реалним координатама x и y, подразумевано (0,0). Могу да се дохвате координате тачке, да се испита да ли се две тачке поклапају (T1==T2) или не (T1!=T2), да се израчуна растојање између две тачке (T1-T2; 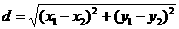) и да се тачка упише у излазни ток (it<<T) у облику (x,y).
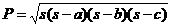• Троугао у равни се задаје са три тачке A, B и C које чине темена троугла, подразумевано ((0,0), (1,0) и (0,1)). Могу да се дохвате темена троугла, да се израчуна површина троугла (; s = (a + b + c) / 2; где су: a, b и c – дужине страница троугла), да се испита да ли су два троугла подударна (t1==t2) или не (t1!=t2; подударна су само ако им се поклапају истоимена темена) и да се троугао упише у излазни ток (it<<t) у облику [A,B,C], где су A, B и C – резултати уписивања темена троугла.
• (30 поена) Скуп троуглова у равни може да садржи произвољан број неподударних троуглова. Ствара се празан, после чега се троуглови додају појединачно (s+=t). Покушај додавања троугла који је подударан неком троуглу у скупу се игнорише. Може да се испита да ли се задати троугао налази у скупу, да се израчуна укупна површина садржаних троуглова и да се скуп упише у излазни ток (it<<s) у облику {t,t,…,t}, где је t – резултат уписивања једног троугла.

(10 поена) Написати на језику C++ програм који направи један скуп, дода му неколико троуглова и испише на главном излазу добијени скуп и укупну провршину троуглова у скупу. Користити фиксне параметре (не треба ништа учитавати с главног улаза).

Решење задатка 2 (⇒ поставка | почетак)

#include <iostream>
#include <cmath>
using namespace std;

class Tacka {
  double x, y;

public:
  explicit Tacka( double xx=0, double yy=0) { x = xx; y = yy; }

  double uzmiX() const { return x; }

  double uzmiY() const { return y; }

  bool operator==( const Tacka& T2) const { return x==T2.x && y==T2.y; }

  bool operator!=( const Tacka& T2) const { return x!=T2.x || y!=T2.y; }

  double operator-(const Tacka& T2) const
    { return sqrt( pow( x-T2.x, 2) + pow( y-T2.y, 2)); }

  friend ostream& operator<<( ostream& it, const Tacka& T)
    { return it << '(' << T.x << ',' << T.y << ')'; }
};

class Trougao {
  Tacka A, B, C;

public:
  explicit Trougao( const Tacka& AA=Tacka(), const Tacka& BB=Tacka(1,0),
                    const Tacka& CC=Tacka(1,0)): A(AA), B(BB), C(CC) {}

  Tacka uzmiA() const { return A; }

  Tacka uzmiB() const { return B; }

  Tacka uzmiC() const { return C; }

  double P() const {
    double a = B-C, b = C-A, c = A-B;
    double s = (a + b + c) / 2;
    return sqrt( s*(s-a)*(s-b)*(s-c));
  }

  bool operator==(const Trougao& t2)const
    { return A==t2.A && B==t2.B && C==t2.C; }

  bool operator!=(const Trougao& t2)const { return ! (*this == t2); }

  friend ostream& operator<< ( ostream& it, const Trougao& t)
    { return it << '[' << t.A << ',' << t.B << ',' << t.C << ']'; }
};

class Skup {
  struct Elem {
    Trougao t;
    Elem* sled;
    Elem( const Trougao& tt): t(tt), sled(0) {}
  };

  Elem *prvi, *posl;

  void kopiraj( const Skup& s);

  void brisi();

public:
  Skup() { prvi = posl = 0; }

  Skup( const Skup& s) { kopiraj( s); }

  ~Skup() { brisi(); }

  Skup& operator=( const Skup& s) {
    if (this != &s){brisi(); kopiraj(s);}
    return *this;
  }

  bool ima( const Trougao& t) const;

  Skup& operator+=( const Trougao& t);

  double ukP() const;

  friend ostream& operator<< ( ostream& it, const Skup& s);
};

void Skup::kopiraj( const Skup& s) {
  prvi = posl = 0;
  for (Elem *tek=s.prvi; tek; tek=tek->sled)
    posl = (!prvi ? prvi : posl->sled) = new Elem( tek->t);
}

void Skup::brisi() {
  while (prvi) { Elem* stari = prvi; prvi = prvi->sled; delete stari; }
  posl = 0;
}

bool Skup::ima( const Trougao& t) const {
  for (Elem* tek=prvi;tek;tek=tek->sled)
    if (tek->t == t) return true;
  return false;
}

Skup& Skup::operator+=(const Trougao& t){
  if (! ima(t))
    posl = (!prvi ? prvi : posl->sled) = new Elem( t);
  return *this;
}

double Skup::ukP() const {
  double p = 0;
  for (Elem* tek=prvi;tek;tek=tek->sled) p += tek->t.P();
  return p;
}

ostream& operator<< ( ostream& it, const Skup& s) {
  it << '{';
  for (Skup::Elem* tek=s.prvi; tek; tek=tek->sled) {
    it << tek->t;
    if (tek->sled) it << ',';
  }
  return it << '}';
}

int main() {
  Skup s;
  s += Trougao ( Tacka(1,1), Tacka (2,5), Tacka(4,3));
  s += Trougao ( Tacka(-1,1), Tacka (-2,5), Tacka(-4,3));
  s += Trougao ( Tacka(1,1), Tacka (2,5), Tacka(4,3));
  s += Trougao ( Tacka(-1,1), Tacka (-2,5), Tacka(-4,3));
  cout << s << endl << s.ukP() << endl;
  return 0;
}

{[(1,1),(2,5),(4,3)],[(-1,1),(-2,5),(-4,3)]}
10

Copyright © 2015, Laslo Kraus
Последња ревизија: 26.6.2015.